Red-Black Tree, RB Tree : 자가 균형 이진 탐색 트리. 연관 배열 등을 구현하는 데 쓰이는 자료 구조이다.
*이진탐색트리(Binary Search Tree)
: 특정 key 값에 대해서 삽입,삭제,탐색이 가능한 자료구조이다.
: 자신의 왼쪽 서브트리에는 현재 노드보다 Key 값이 작은 것, 오른쪽 서브트리에는 Key 값이 큰 것들로 구성된다.

| Red-Black Tree = Balanced binary search tree |
Red-Black Tree = Balanced binary search tree 로 위와 같은 모양이 나오지 않도록 "조건"을 건다.
Rea-Black Tree의 높이=log n 에 바운드 됨, search 연산은 O(log n)의 시간 복잡도를 가지게 된다.
| 특징 |
1. Root Property : Root node의 색은 Black.
2. External Property : 모든 external node들은 Black.
3. Internal Property : Red node의 자식은 Black. ==> No Double Red. Red node는 연속으로 나올 수 없다. RED의 자식은 Black.
4. Depth Property : 모든 leaf node에서 Black Depth는 같다. ==> leaf node에서 Root node까지 가는 경로에서 만나는 Black node의 개수는 같다.
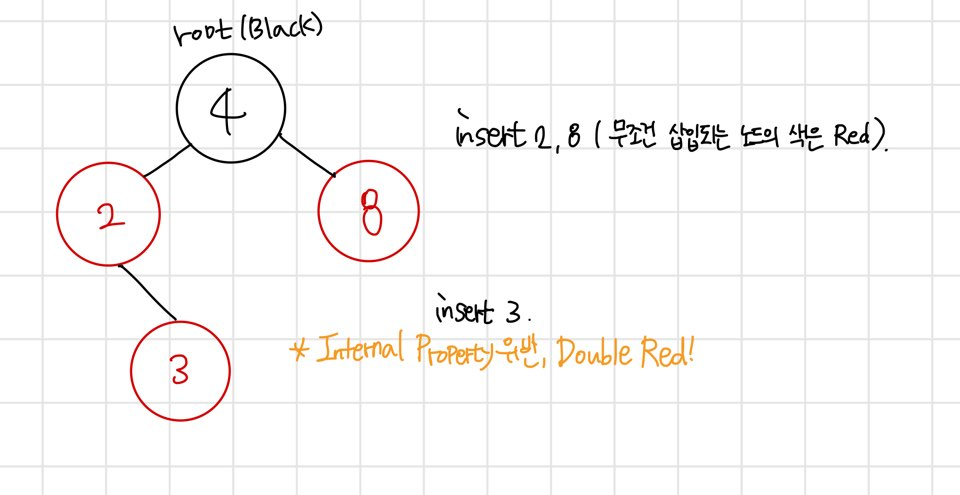
위 그림과 같이 Double Red 발생시!
해결 전략
◆Restructuring
◆Recoloring
* insert된 노드의 uncle node(부모의 형제노드) 'x' 의 색에 따라 프로시저가 다르다.
x = Black : Restructuring. Red : Recoloring 수행.
◆Restructuring
현재 insert된 노드(a)와 부모(b), 부모의 부모(Grand Parent, c)를 가지고 Restructuring 수행. 재건축 !!
1. 나(a), 내 부모(b), 부모의 부모 (c)를 오름차순으로 정렬
2. 가운데 있는 값을 부모로 만들고 나머지 둘을 자식으로 만든다.
3. 올라간 가운데에 있는 값을 Black으로 만들고 두 자식들을 Red로 만든다.

◆Recoloring
1. 현재 insert된 노드(a)의 부모(b)와 그 형제(x)를 Black으로 하고 Grand Parent(c) 를 Red로 한다.
2. Grand Parent(c)가 Root node가 아니었을 시 Double Red가 다시 발생 할 수 있다.


Red-Black Tree에 insertion하는 경우 Restructuring, Recoloring 모두 O(logn)이 걸린다.
==> Balanced.
Depth Property = 어느 leaf node에서 Root node까지 가더라도 Black Depth는 항상 같아야 한다.
1. 가장 짧은 Black Depth를 가지는 external node와 가장 긴 Black Depth를 가지는 external node의 Black Depth는 같아야 하면서 가장 짧아야 한다. (Black node만 있다)
2. Black Depth는 같으면서 가장 길려면 B-R-B-R-B-R...-B 로 이루어져야 한다.
1과 2의 높이 차이는 최대 2배이므로 Balance함.
Depth Property로 인해 높이가 logn에 바운드 될 수 있다.
'논문 리뷰 > Accelerating Dynamic Graph Analytics on' 카테고리의 다른 글
| Thread (0) | 2020.11.26 |
|---|---|
| Synchronization (0) | 2020.11.25 |
| Muex (0) | 2020.11.25 |